I det första inlägget i denna serie om DCF gick vi igenom grunderna i DCF-värdering. I förra inlägget såg vi vilka motiverade P/E-tal som DCF-modellen ger upphov till vid olika parameterval. I detta inlägg gör vi ett kort utvik för att göra en jämförelse med Grahams formel P/E=8,5+2g.
I kapitel 11 av The Intelligent Investor föreslår Graham att värdet av ett bolag på ett förenklat sätt kan beskrivas som P/E=8,5+2g där g är tillväxttakten de kommande 7-10 åren. Denna formel är en förenkling av DCF och nedan tänkte jag visa kort vilka parametrar som jag tror att Graham använde sig av för att få fram approximationen samt jämföra med DCF. Grahams formel är en linjär funktion medan DCF är exponentiell, så vid höga tillväxttal borde skillnaden bli som störst.
Via lite experimenterande så menar jag att det är möjligt att Graham använde ungefär följande parametrar:
- Diskonteringsränta 10,5 %. Den sista utgåvan av The Intelligent Investor som Graham lade sin hand vid uppdaterades 1971-1972 då ränteläget var högre än idag. Under 1960-talet låg AAA bond rate kring 4 % för att i början av 1970-talet stiga mot 8 %. 10,5 % gav viss marginal mot den säkra räntan.
- Tillväxt 3 % per år efter de första 7-10 åren (om tillväxten de första 7-10 åren överskrider 3 %). För lägre tillväxt än så under de första 7-10 åren så antas också en lägre tillväxt efter de första 7-10 åren. Om man exempelvis sätter 0 % tillväxt under de första 7-10 åren så gör man det för resten av tiden också.
- Tillväxten de första 7-10 åren är en variabel i Grahams formel.
Kommentar till ovanstående: Graham skriver faktiskt i kapitlet att om man antar en tillväxt på 8 % per år mot oändligheten så blir värderingen oändlig. Det tyder på att han använde en diskonteringsränta på strax under 8 %.
Ännu längre bak i kapitlet så skriver Graham att räntesatserna har varierat över åren och att dessa påverkar värderingen (via diskonteringsräntan). Därför använder han den ”gamla” formeln P/E=8,5+2g eftersom den uppskattar värdet lika bra som något annat över tid. Formeln verkar alltså ha hängt med sedan längre bak i tiden än utgåvan från 1970-talet vilket också innebär att räntan var lägre då.
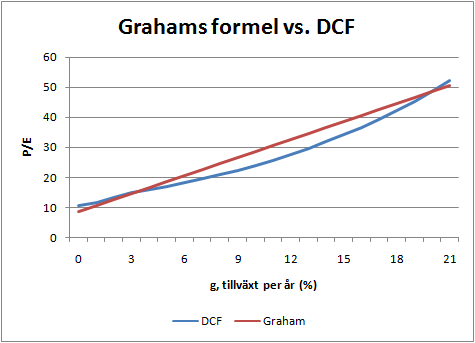
En jämförelse mellan Grahams formel och DCF med ovanstående antaganden ser ut som följer:
Grahams formel underskattar värdet något vid låga tillväxttakter men överskattar värdet något (men endast med några ”P/E-enheter”). Som störst är skillnaden 5 P/E-enheter vid tillväxttakter kring 12-13 % per år. Vid extremt höga tillväxttakter över ca 20 % per år i 10 år (dvs. i princip mer än en sexdubbling av resultatet på så kort tid) så ger DCF högre värden för att därefter skena iväg, vilket har klippts bort ur figuren. Högre tillväxttakter än så under 7-10 år ser man inte ofta.
Om man justerar diskonteringsräntan lite så flyttar sig DCF-kurvan upp eller ned och det kan lika väl vara så att Graham antog en något lägre diskonteringsränta för att inte överskatta värdet vid tillväxt mellan 4-20 % per år. Å andra sidan så är det en grov tumregel som säkert fungerar bra i många fall och ett sätt att lägga in säkerhetsmarginal i Grahams formel är att bedöma tillväxttakten försiktigt.
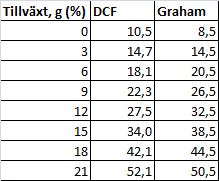
Vi tar jämförelsen i tabellform också om någon vill läsa av enskilda värden eller gillar tabeller bättre än figurer.
Avslutningsvis så kan jag nämna att bloggrannen Lundaluppen har en annan teori om hur Graham konstruerade sin formel med 6 % diskonteringsränta och att endast värdet från 20 år av vinster tas med. Det ger ungefär likvärdiga resultat (speciellt om man sätter tillväxten år 11-20 till 3 %). 6 % diskonteringsränta innehåller dock ingen säkerhetsmarginal överhuvudtaget och i sådana fall bör man tillämpa rejäl säkerhetsmarginal på tillväxtfaktorn istället. Klart är i alla fall att man kan lägga in säkerhetsmarginal både här och där i en DCF-modell och det går att åstadkomma samma resultat på många olika sätt. Till exempel genom att antingen sätta en högre diskonteringsränta eller att ta bort oändlighetsvärdet. Jag får upprepa budskapet att om man ska använda DCF för aktievärdering så måste man vara konsekvent med sina antaganden om parametervärden för att inte lura sig själv och motivera felaktiga värden.
Detta inlägg var en kort utvikning efter lite laborerande med DCF och Grahams formel. I det sista inlägget i serien om DCF-värdering så ska vi se vilket motiverat värde H&M kan tänkas ha vid olika antaganden om parametervärden.
En alldeles tillräcklig approximation med andra ord, speciellt om vi betänker att arbetet att beräkna DCF för hand (vi talar om 40-, 50 och 60-tal) med exponentialfunktioner kan få de flesta ur balans efter en analys av sådär 30 bolag eller fler. Visst, den tidens hjälpmedel som tabeller och räknesticka hjälpte en del men det är ju långt, långt till miniräknare, datorer och Excelark om vi säger så. Prova själv att handjaga de exempel som beskrevs i föregående inlägg. Hur många kan beräkna 1.08 upphöjt till sju i huvudet och invertera resultatet och för de som inte klarar det: hur lång tid tar det att göra det med papper och penna?
Inom många andra arbetsområden är (och var) en linjärisering av exponentialfunktioner vanliga men, som vanligt, så måste den som använder förenklingarna känna till när de går att tillämpa och vilka avvikelser som vi har iom linjärisering.
Jag ser det som ett utmärkt sett att få en uppfattning – ”känsla” – för vad som är rimligt för ett bolags aktie. Jag behöver ju inte veta på kilot vad en person väger för att bedöma om en person är överviktig eller inte, den bedömningen gör men lätt ändå (för att ta en Buffett tumregel)
Ja, Sten. Grahams approximation duger alldeles utmärkt även om man har Excel och annat :-) Däremot var nog folk bättre på huvudräkning förr i tiden och räknestickan verkar genial även om jag som 80-talist tycker det minst sagt är en mystisk pryl. Men linjära funktioner och lösa ut g i huvudet från P/E=8,5+2g kan nog till och med de flesta idag som har läst första mattekursen på gymnasiet.
Minns jag rätt från matten så går väl alla funktioner att utveckla till ett antal polynom och för små värden så approximeras alla funktioner som linjära. En gammal hederlig andragradare hade förmodligen varit grymt bra att approximera DCF för tillväxt större än noll, men börjat balla ur för tillväxt lägre än noll ;-)
Instämmer i övrigt. Det som jag saknar med Grahams formel är att den inte tar hänsyn till skuldsättning, utan ett skuldtyngt bolag ser ut att vara lika mycket värt till P/E 10 som ett skuldfritt bolag med samma P/E-multipel. Detta finns det lite andra nyckeltal som tar hand om (EV/EBIT och liknande) och det kommer i ett inlägg så småningom då jag har varit obekväm att använda Grahams formel för hårt skuldsatta bolag – med all rätta lär det visa sig.