Gordons formel och Lászlós formel

I senaste numret av Aktiespararen finns en artikel om börsprofilen László Szombatfalvy. Artikeln finns tyvärr inte på nätet om man inte är medlem. László blev förmögen på aktiemarknaden genom en egenutvecklad värderingsmodell. Enligt Aktiespararens artikel visade det sig att en av formlerna László använde var identisk med Gordons formel. I artikeln beskrivs även en annan formel som vi här kallar för Lászlós formel. Formlernas syfte är att hitta en värdering av bolag. Detta inlägg beskriver formlerna och tillämpar formlerna på några bolag.

Inlägget tar inte upp kritik mot modellerna utan inledningsvis räcker det att konstatera att alla modeller har brister. En kritisk granskning av Lászlós värderingsmodell gör däremot Riskminimeraren i detta inlägg.

Gordons formel

Gordons formel värderar ett företag utifrån DCF-modellen och formeln ser ut enligt följande:

P = d / (k-g)

där
P = motiverad börskurs
d = utdelning
k = avkastningskrav
g = tillväxttakten hos utdelningen

k och g ska inte anges i procent, utan bara som ett tal (dvs. 5 % ska anges som 0,05). Läs även om Gordons formel på Inkomsten eller Wikipedia. Investeringsinspektören skriver också intressant om DCF.

Modellen har som alla modeller sina nackdelar. Om k är nära g så går börsvärdet mot oändligheten vilket också innebär att ju närmare k och g är varandra, desto känsligare blir metoden. Modellen antar också evig tillväxt. Vi tänkte dock inte gå in i modellen på djupet så kritiken stannar här.

Lászlós formel

László utvecklade Gordons formel till sin egen formel – Lászlós formel. Istället för utdelning i Gordons formel så använder László utdelningskapaciteten, dvs. den del av vinsten som inte behöver behållas i företaget för att öka det egna kapitalet i takt med att rörelsen växer. László översätter inte fritt kassaflöde (FCF) direkt till utdelningskapacitet, utan beräknar det på ett omständigare sätt. Lászlós modell utgår från att utdelning, börskurs, eget kapital och balansomslutning växer i samma takt (dvs. konstant direktavkastning och konstant soliditet).

Lázsló räknar ut utdelningskapaciteten på följande sätt. Om balansomslutningen (eller det egna kapitalet, eller justerat eget kapital) växer med en viss takt per år så antar han att lika mycket måste återinvesteras i verksamheten (capex) varje år. Detta jämförs sedan med avkastning på justerat eget kapital (JEK). Avkastning på justerat eget kapital beräknas som vinst/JEK. Utdelningskapaciteten definieras därefter enligt följande:

Utdelningskapacitet = (Avkastning på JEK – tillväxt av JEK)*JEK

Lászlós formel ser således ut precis som Gordons formel men faktorerna betyder något annat enligt följande:

P = d / (k-g)

där
P = motiverad börskurs
d = Utdelningskapacitet = (Avkastning på JEK – Tillväxt av JEK)*JEK
Avkastning på JEK = JEK/Vinst
k = avkastningskrav
g = tillväxttakten hos JEK

Även här ska k och g anges som tal och inte som procent.

Frågan är varför László inte använder fritt kassaflöde som utdelningskapacitet? Det borde vara enklare i vissa fall, men i andra fall är det förmodligen så att investeringarna kan fluktuera väldigt över tid så att nyckeltalen baserade på eget kapital ger jämnare värden. Vill man tillämpa Lászlós formel borde man alltså kunna använda fritt kassaflöde som utdelningskapacitet om det är enklare att bedöma, vilket säkert varierar från fall till fall.

Exempel och jämförelse mellan Gordons och Lászlós formler

I samtliga exempel nedan har för enkelhets skull eget kapital använts istället för justerat eget kapital. Eget kapital är enklare att hitta och skillnaden borde inte bli särskilt stor för de valda bolagen.

Exempel 1 – Axfood

Axfoods utdelning har de tio senaste åren ökat från ingen utdelning (nystartat bolag) till 12 kr per år. Grovt räknat så kan man säga att utdelningen har ökat med ca 10 % per år. Detta är dock inte fallet för de senaste åren och det kommer heller inte vara fallet i framtiden, så istället väljs en ökning med 3 % per år.

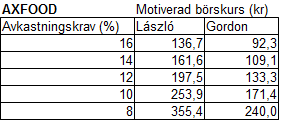
Även det egna kapitalet har växt 3 % per år. Nedan visas riktkurser med Lászlós formel och Gordons formel för Axfood med några olika avkastningskrav:

För ett visst avkastningskrav kan man få en motiverad börskurs. Omvänt kan man se vilken avkastning man kan förvänta sig vid en viss börskurs. Nuvarande börskurs (14 november 2011) är ca 240 kr vilket innebär att man kan förvänta sig en årlig avkastning på ca 10 % enligt Lászlós formel eller 8 % enligt Gordons formel. Dagens värdering är alltså möjlig att förstå via båda formlerna med lite olika avkastningskrav.

Siffror som har använts i Gordons formel för Axfood är följande:

d = Utdelning = 12 kr/aktie (utdelning 2010).
k = avkastningskrav = se tabellen ovan
g = tillväxttakten hos utdelningen = 3 %/år

Siffror som har använts i Lászlós formel för Axfood är följande:

d = Utdelningskapacitet = (Avkastning på JEK – Tillväxt av JEK)*JEK = (34,4 – 3,0) * 56,4 = 17,8 (kr/aktie). Detta är betydligt högre än de 12 kr/aktie som delades ut 2010.
k = avkastningskrav = se tabellen ovan
g = tillväxttakten hos JEK = 3,0 %/år

Exempel 2 – Skåne-Möllan

Skåne-Möllans utdelning har de tio senaste åren ökat med ca 25 % per år. Detta är dock inte långsiktigt hållbart, så istället tas de senaste tre årens utdelningsökning på ca 5,7 % per år.

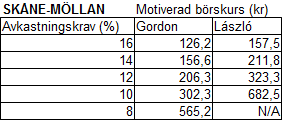
Det egna kapitalet har växt ca 8,2 % per år under de senaste fem åren.Nedan visas riktkurser med Lászlós formel för Skåne-Möllan med några olika avkastningskrav:

Nuvarande börskurs (14 november 2011) är drygt 360 kr vilket innebär att man kan förvänta sig en årlig avkastning på ca 11 % enligt Lászlós formel om det egna kapitalet fortsätter att växa som de senaste tio åren med konstant avkastning på eget kapital. Gordon är i detta fall mer pessimistisk och utlovar endast ca 9 % per år. Dagens värdering är alltså möjlig att förstå med båda formlerna med lite olika avkastningskrav.

Siffror som har använts i Gordons formel för Skåne-Möllan är följande:

d = Utdelning = 13 kr/aktie (utdelning 2010).
k = avkastningskrav = se tabellen ovan
g = tillväxttakten hos utdelningen = 5,9 %/år

Siffror som har använts i Lászlós formel för Skåne-Möllan är följande:

d = Utdelningskapacitet = (Avkastning på JEK – Tillväxt av JEK)*JEK = (18,5 – 8,2) * 119,28 = 12,3 kr/aktie. Denna siffra är något lägre än den verkliga utdelningen 2010.
k = avkastningskrav = se tabellen ovan
g = tillväxttakten hos JEK = 8,2 %/år

Exempel 3 – Fortum

För att Gordons formel ska fungera bra så ska utvecklingen vara något sånär stabil hos utdelningstillväxten. Det är den inte hos Fortum, där utdelningen från 2000-2007 ökade kraftigt från 0,23 €/aktie till 1,35 €/aktie för att därefter minska  och har legat stabilt på 1 €/aktie de senaste åren. Om Fortums utdelningstillväxt skulle väljas från 2000 till 2010 så är utdelningstillväxten 16 % per år vilket absolut inte är hur framtiden kommer att se ut. Hur framtiden ser ut är svårt att säga. Jag hugger till med att utdelningen kommer att öka 3 % per år i framtiden vilket förmodligen inte är heltokigt.

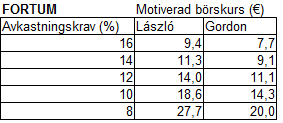
För Lázslós formel är det något mer rakt på sak men även här spelar naturligtvis avkastningskravet stor roll. Nedan visas riktkurser med Lászlós formel för Fortum med några olika avkastningskrav:

Nuvarande börskurs (14 november 2011) är drygt 17 € vilket innebär att man kan förvänta sig en årlig avkastning på ca 11 % enligt Lászlós formel om det egna kapitalet fortsätter att växa som de senaste tio åren med konstant avkastning på eget kapital. Enligt Gordons formel är avkastningen snarare 9 % per år. Dagens värdering är alltså möjlig att förstå med båda formlerna med lite olika avkastningskrav.

Siffror som har använts i Gordons formel för Fortum är följande:

d = Utdelning = 1 €/aktie (utdelning 2010).
k = avkastningskrav = se tabellen ovan
g = tillväxttakten hos utdelningen = 3 %/år

Siffror som har använts i Lászlós formel för Fortum är följande:

d = Utdelningskapacitet = (Avkastning på JEK – Tillväxt av JEK)*JEK = (16,2 – 3,9) * 9,24 = 1,1 (€/aktie)
k = avkastningskrav = se tabellen ovan
g = tillväxttakten hos JEK = 3,9 %/år

Slutsatser

Både Lászlos och Gordons formel ger upphov till dagens börskurser om man väljer ett avkastningskrav kring 10 %. 10 % är också vad Investeringsinspektören väljer vid DCF-värdering vilket verkar rimligt utifrån dessa exempel. Har man ett annat avkastningskrav är det naturligtvis bara att använda det istället i formlerna.

Den stora svårigheten med båda formlerna är naturligtvis att bedöma nyckelparametrarna. Vilken formel som fungerar bäst varierar förmodligen från fall till fall.

I Lászlós formel är en nyckelparameter avkastning på justerat eget kapital vilket kan innebära att bolag med lite eget kapital (låg soliditet=stor hävstång) premieras. Exempel på bolag som skulle bli högt värderade med Lászlós formel är förmodligen Swedish Match och Getinge som båda har mycket litet eget kapital (i själva verket negativt eget kapital exklusive goodwill). I formeln måste man även bedöma tillväxten på eget kapital.

I Gordons formel är en nyckelparameter istället utdelningstillväxten, vilken kan vara svåruppskattad. Det gäller här att hålla koll så att ett bolag inte upprätthåller en hög utdelningstillväxt genom att ta upp lån, något som inte är hållbart i längden.

Av exemplen att döma så borde formlerna kunna tillämpas för att hitta grovt under- eller övervärderade bolag. Däremot är det knappast rimligt att använda formlerna för att säga om ett bolags aktie är värd 200 eller 225 kr.